Neutrino Physics

Implications of neutrino mass

3. Fermions weigh in 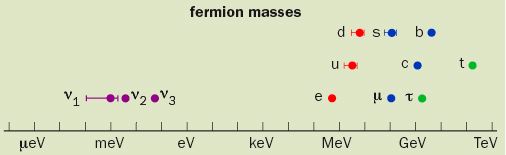A comparison of the masses of all the fundamental fermions, particles with spin 1/2. Other than the neutrino, the lightest fermion is the electron, with a mass of 0.5 MeV/c2. Neutrino-oscillation experiments do not measure the mass of neutrinos directly, rather the mass difference between the different types of neutrino. But by assuming that neutrino masses are similar to this mass difference, we can place upper limits on the mass of a few hundred millielectron-volts.

Now that neutrinos do appear to have mass, we have to solve two problems. The first is to overcome the contradiction between left-handedness and mass. The second is to understand why the neutrino mass is so small compared with other particle masses — indeed, direct measurements indicate that electrons are at least 500 000 times more massive than neutrinos. When we thought that neutrinos did not have mass, these problems were not an issue. But the tiny mass is a puzzle, and there must be some deep reason why this is the case.

Basically, there are two ways to extend the Standard Model in order to make neutrinos massive. One approach involves new particles called Dirac neutrinos, while the other approach involves a completely different type of particle called the Majorana neutrino.

The Dirac neutrino is a simple idea with a serious flaw. According to this approach, the reason that right-handed neutrinos have escaped detection so far is that their interactions are at least 26 orders of magnitude weaker than ordinary neutrinos. The idea of the Dirac neutrino works in the sense that we can generate neutrino masses via the Higgs mechanism (figure 2b). However, it also suggests that neutrinos should have similar masses to the other particles in the Standard Model. To avoid this problem, we have to make the strength of neutrino interactions with the Higgs boson at least 12 orders of magnitude weaker than that of the top quark. Few physicists accept such a tiny number as a fundamental constant of nature.

2. Neutrinos meet the Higgs boson 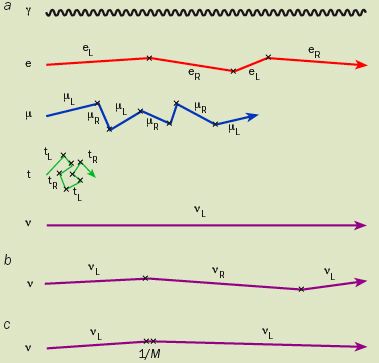(a) According to the Higgs mechanism in the Standard Model, particles in the vacuum acquire mass as they collide with the Higgs boson. Photons (γ) are massless because they do not interact with the Higgs boson. All particles, including electrons (e), muons (μ) nd top quarks (t), change handedness when they collide with the Higgs boson; left-handed particles become right-handed and vice versa. Experiments have shown that neutrinos (ν) are always left-handed. Since right-handed neutrinos do not exist in the Standard Model, the theory predicts that neutrinos can never acquire mass. (b) In one extension to the Standard Model, left- and right-handed neutrinos exist. These Dirac neutrinos acquire mass via the Higgs mechanism but right-handed neutrinos interact much more weakly than any other particles. (c) According to another extension of the Standard Model, extremely heavy right-handed neutrinos are created for a brief moment before they collide with the Higgs boson to produce light left-handed Majorana neutrinos.

An alternative way to make right-handed neutrinos extremely weakly interacting was proposed in 1998 by Nima Arkani-Hamed at the Stanford Linear Accelerator Center, Savas Dimopoulous of Stanford University, Gia Dvali of the International Centre for Theoretical Physics in Trieste and John March-Russell of CERN. They exploited an idea from superstring theory in which the three dimensions of space with which we are familiar are embedded in 10- or 11-dimensional spacetime. Like us, all the particles of the Standard Model — electrons, quarks, left-handed neutrinos, the Higgs boson and so on — are stuck on a three-dimensional "sheet" called a three-brane.

One special property of right-handed neutrinos is that they do not feel the electromagnetic force, or the strong and weak forces. Arkani-Hamed and collaborators argued that righthanded neutrinos are not trapped on the three-brane in the same way that we are, rather they can move in the extra dimensions. This mechanism explains why we have never observed a right-handed neutrino and why their interactions with other particles in the Standard Model are extremely weak. The upshot of this approach is that neutrino masses can be very small.

The second way to extend the Standard Model involves particles that are called Majorana neutrinos. One advantage of this approach is that we no longer have to invoke righthanded neutrinos with extremely weak interactions. However, we do have to give up the fundamental distinction between matter and antimatter. Although this sounds bizarre, neutrinos and antineutrinos can be identical because they have no electric charge.

Massive neutrinos sit naturally within this framework. Recall the observer travelling at the speed of light who overtakes a left-handed neutrino and sees a right-handed neutrino. Earlier we argued that the absence of right-handed neutrinos means that neutrinos are massless. But if neutrinos and antineutrinos are the same particle, then we can argue that the observer really sees a right-handed antineutrino and that the massive-neutrino hypothesis is therefore sound.

So how is neutrino mass generated? In this scheme, it is possible for right-handed neutrinos to have a mass of their own without relying on the Higgs boson. Unlike other quarks and leptons, the mass of the right-handed neutrino, M, is not tied to the mass scale of the Higgs boson. Rather, it can be much heavier than other particles.

When a left-handed neutrino collides with the Higgs boson, it acquires a mass, m, which is comparable to the mass of other quarks and leptons. At the same time it transforms into a right-handed neutrino, which is much heavier than energy conservation would normally allow (figure 2c). However, the Heisenberg uncertainty principle allows this state to exist for a short time interval, Δt, given by Δt ~h/Mc², after which the particle transforms back into a left-handed neutrino with mass m by colliding with the Higgs boson again. Put simply, we can think of the neutrino as having an average mass of m²/M over time.

This so-called seesaw mechanism can naturally give rise to light neutrinos with normal-strength interactions. Normally we would worry that neutrinos with a mass, m, that is similar to the masses of quarks and leptons would be too heavy. However, we can still obtain light neutrinos if M is much larger than the typical masses of quarks and leptons. Right-handed neutrinos must therefore be very heavy, as predicted by grandunified theories that aim to combine electromagnetism with the strong and weak interactions.

Current experiments suggest that these forces were unified when the universe was about 10³² m across. Due to the uncertainty principle, the particles that were produced in such small confines had a high momentum and thus a large mass. It turns out that the distance scale of unification gives righthanded neutrinos sufficient mass to produce light neutrinos via the seesaw mechanism. In this way, the light neutrinos that we observe in experiments can therefore probe new physics at extremely short distances. Among the physics that neutrinos could put on a firm footing is the theory of supersymmetry, which theorists believe is needed to make unification happen and to make the Higgs mechanism consistent down to such short distance scales.

1. Introduction
   Neutrinos are everywhere. Trillions of them are passing through your body every second,but they are so shy and we do not see or feel them. They are the least understood elementary particle we know that exist.
2. Birth of Neutrinos
   Existing of neutrinos was suggested as a "desperate remedy" to the apparent paradox that the energy did not appear conserved in the world of atomic nuclei.
3. The Standard Model
   The Standard Model of particle physics can describe everything we know about elementary particles. It says that neutrinos do not have mass. Neutrinos do not have mass because they are all "left-handed" and do not bump on the mysterious "Higgs boson" that fills our entire Universe.
4. Evidence for neutrino mass
   In 1998, a convincing evidence was reported that neutrinos have mass. The Standard Model has fallen after decades of invicibility. The evidence comes from experiments deep underground in pitch darkness with many thousands of tonnes of water housed in mines.
5. Implications of neutrino mass
   Neutrinos are found to have mass, but the mass is extremely tiny, at least million times lighter than the lighest elementary particle: electron. How do we need to change the Standard Model to explain the neutrino mass? Some argue that our spacetime has unseen spatial dimensions, and we are stuck on three-dimensional "sheets". Other argue that we need to abandon the sacred distinction between matter and anti-matter.
6. Why do we exist?
   When Universe started with the "Big Bang", there were almost equal amount of matter and anti-matter. Most of matter was annihilated by anti-matter when Universe cooled. We are leftover of one part in ten billions. Why was there a small excess matter over anti-matter so that we can exist? Once we abandon the sacred distinction between matter and anti-matter, it provides a key to understand why we exist.
7. Outlook The mysteries about neutrinos are now being unraveled dramatically. We will learn much more in the coming years.

This homepage is based on Feature Article "Origin of Neutrino mass" in Physics World, May 2002, by Hitoshi Murayama. The whole article can be download as a PDF file.