Introduction to Supersymmetry
Introduction to Supersymmetry
20th century physics has seen two major paradigm shifts in the way we
understand Mother Nature. One is quantum mechanics, and the other is
relativity. The marriage between the two, called quantum field
theory, conceived an enfant terrible, namely
anti-matter. As a result, the number of elementary particles
doubled. We believe that 21st century physics is aimed at yet another
level of marriage, this time between quantum mechanics and general
relativity, Einstein's theory of gravity. The couple has not been
getting along very well, resulting in mathematical inconsistencies,
meaningless infinities, and negative probabilities. The key to
success may be in supersymmetry, which doubles the number of
particles once more.
Why was anti-matter needed? One reason was to solve a crisis in the
19th century physics of classical electromagnetism. An electron is,
to the best of our knowledge, a point particle. Namely, it has no
size, yet an electric charge. A charged particle inevitably produces
an electric potential around it, and it also feels the potential
created by itself. This leads to an infinite "self-energy" of the
electron. In other words, it takes substantial energy to "pack" all
the charge of an electron into small size.
On the other hand, Einstein's famous equation 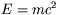 says that mass of a particle determines the energy of
the particle at rest. For an electron, its rest energy is known to be
0.511 MeV. For this given amount of energy, it cannot afford to
"pack" itself into a size smaller than the size of a nucleus.
Classical theory of electromagnetism is not a consistent theory below
this distance. However, it is known that the electron is at
least ten thousand times smaller than that.
says that mass of a particle determines the energy of
the particle at rest. For an electron, its rest energy is known to be
0.511 MeV. For this given amount of energy, it cannot afford to
"pack" itself into a size smaller than the size of a nucleus.
Classical theory of electromagnetism is not a consistent theory below
this distance. However, it is known that the electron is at
least ten thousand times smaller than that.
(a) 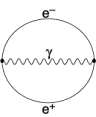 (b)
(b) 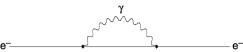 (c)
(c) 
What saved the crisis was the existence of anti-matter, positron.
In quantum mechanics, it is possible to "borrow" energy within the time
interval allowed by the uncertainty principle. Once there exists
anti-matter, which can annihilate matter or be created with matter,
what we consider to be an empty vacuum undergoes a fluctuation to
produce a pair of electron and positron together with photon,
annihilating back to vacuum within the time interval allowed by the
uncertainty principle (a). In addition to the effect of the electric
potential on itself (b), the electron can annihilate with a positron
in the fluctuation, leaving the electon originally in the fluctuation
to materialize as a real electron (c). It turns out, these two
contributions to the energy of the electron almost nearly cancel with
each other. The small size of the electron was made consistent with
electromagnetism thanks to quantum mechanics and the existence of
anti-matter.
 Currently the Standard Model of particle physics is
facing a similar crisis. We know that our Universe is filled with a
mysterious condensate of Higgs boson, which disturbs matter particles
and forces, not letting them go far and hence making them massive.
For example, the carrier of the weak force, W boson, bumps on the
Higgs condensate all the time, and the force has become short-ranged,
extending only over a thoughsandth of the size of nuclei. All masses
of known elementary particles must have come from the Higgs boson.
However, the mass of the Higgs boson receives a large contribution
from its interaction with itself making it impossible for us to study
physics at smaller distances. Because the gravity is believed to be
unified with other forces at an extremely small distance called Planck
length
Currently the Standard Model of particle physics is
facing a similar crisis. We know that our Universe is filled with a
mysterious condensate of Higgs boson, which disturbs matter particles
and forces, not letting them go far and hence making them massive.
For example, the carrier of the weak force, W boson, bumps on the
Higgs condensate all the time, and the force has become short-ranged,
extending only over a thoughsandth of the size of nuclei. All masses
of known elementary particles must have come from the Higgs boson.
However, the mass of the Higgs boson receives a large contribution
from its interaction with itself making it impossible for us to study
physics at smaller distances. Because the gravity is believed to be
unified with other forces at an extremely small distance called Planck
length 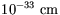 , the marriage between quantum mechanics
and gravity appears a remote dream.
, the marriage between quantum mechanics
and gravity appears a remote dream.
Supersymmetry is an idea that history repeats itself to solve
similar problems. For every particle, there is a superpartner whose
spin differs by 1/2. By doubling the number of particles again, there
is similar cancellation between the process with ordinary particles
only and another process with their superpartners. Then the Standard
Model can describe physics down to the Planck length, making the
marriage a realistic hope. In fact, it is a necessary ingredient in
the only available candidate for quantum theory of gravity, string
theory.
(a)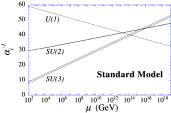 (b)
(b)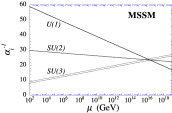
Supersymmetry actually makes the unification of three other
forces, strong, weak, and electromagnetic, also a reality. In (a), in
the Standard Model without supersymmetry, the strengths of three
forces change as a function of energies, and become closer to each
other at very high energies. Together with supersymmetry (Minimal
Supersymmetric Standard Model or MSSM), however, they become equal
within a percent-level accuracy.
Where are superpartners? It is a realistic hope that coming
accelerator experiments will find them, possibly Tevatron collider at
Fermilab, Illinois, or the Large Hadron Collider at CERN, Geneva,
Switzerland in this decade.
(a) 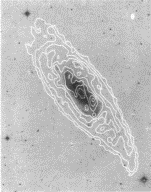 (b)
(b) 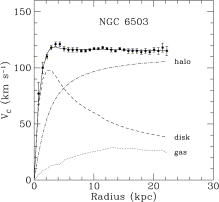
It is amusing that superpartners may actually be everywhere without us
noticing. Our galaxy is known to be full of Dark Matter, weakly
interacting particles whose gravitational pull binds the galaxy
together despite its fast rotation. The picture (a) shows the
measurement of Doppler shift in 21cm line that allows us to determine
the rotational speed of other galaxies. The rotational speed is much
faster than what the gravitional pull by stars would allow (b). One
of the best candidates for Dark Matter is the lightest supersymmetric
particle.
Even though supersymmetry solves many problems in particle physics, it
also poses new problems.
- What makes superpartners heavier than ordinary particles? This
is the problem of supersymmetry breaking.
- Why are superpartners so well hidden in rare phenomena?
Arbitrary mass spectrum of superpartners actually would cause too
large effects in rare processes that change flavor of particles.
There must be some special reason why such effects are well hidden.
- How do we discover superpartners experimentally? How do we
extract information on the mechanism of supersymmetry breaking?
- How does supersymmetry impact cosmology? Is the lightest
supersymmetric partner the Dark Matter? How do we prove it?
We are working on these problems.
Our group had made substantial contributions to the theoretical
study of supersymmetry. It was Bruno
Zumino, together with Julius Wess, who discovered the possibility
of supersymmetry in four-dimensional spacetime back in 1973.
Until early 1980's, however, it was more of a mathematical curiosity
than a serious possibility for the realistic theory of nature. Lawrence
Hall, together with Joe Lykken and Steven Weinberg, laid the
foundation of relatistic supersymmetric phenomenology. Mary
K Gaillard made it possible to systematically study quantum
effects in supersymmetric theory of gravity, supergravity. Hitoshi Murayama, together with
Gian Giudice and two former Berkeley postdocs, Markus Luty and
Riccardo Rattazzi, found subtle quantum contributions to masses of
superpartners, independently with two other former Berkeley postdocs,
Lisa Randall and Raman Sundrum.
This home page is based on the introduction in Supersymmetry
Phenomenology by Hitoshi Murayama.
-
murayama@physics.berkeley.edu
- Phone (510) 486 5589, Campus phone (510)
642-1019
- Location Bldg. 50A 5109 (LBL), 447 Birge (Campus)

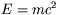 says that mass of a particle determines the energy of
the particle at rest. For an electron, its rest energy is known to be
0.511 MeV. For this given amount of energy, it cannot afford to
"pack" itself into a size smaller than the size of a nucleus.
Classical theory of electromagnetism is not a consistent theory below
this distance. However, it is known that the electron is at
least ten thousand times smaller than that.
says that mass of a particle determines the energy of
the particle at rest. For an electron, its rest energy is known to be
0.511 MeV. For this given amount of energy, it cannot afford to
"pack" itself into a size smaller than the size of a nucleus.
Classical theory of electromagnetism is not a consistent theory below
this distance. However, it is known that the electron is at
least ten thousand times smaller than that.
 (b)
(b) 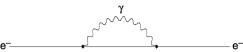 (c)
(c) 
 Currently the Standard Model of particle physics is
facing a similar crisis. We know that our Universe is filled with a
mysterious condensate of Higgs boson, which disturbs matter particles
and forces, not letting them go far and hence making them massive.
For example, the carrier of the weak force, W boson, bumps on the
Higgs condensate all the time, and the force has become short-ranged,
extending only over a thoughsandth of the size of nuclei. All masses
of known elementary particles must have come from the Higgs boson.
However, the mass of the Higgs boson receives a large contribution
from its interaction with itself making it impossible for us to study
physics at smaller distances. Because the gravity is believed to be
unified with other forces at an extremely small distance called Planck
length
Currently the Standard Model of particle physics is
facing a similar crisis. We know that our Universe is filled with a
mysterious condensate of Higgs boson, which disturbs matter particles
and forces, not letting them go far and hence making them massive.
For example, the carrier of the weak force, W boson, bumps on the
Higgs condensate all the time, and the force has become short-ranged,
extending only over a thoughsandth of the size of nuclei. All masses
of known elementary particles must have come from the Higgs boson.
However, the mass of the Higgs boson receives a large contribution
from its interaction with itself making it impossible for us to study
physics at smaller distances. Because the gravity is believed to be
unified with other forces at an extremely small distance called Planck
length 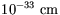 , the marriage between quantum mechanics
and gravity appears a remote dream.
, the marriage between quantum mechanics
and gravity appears a remote dream.
 (b)
(b)
 (b)
(b)